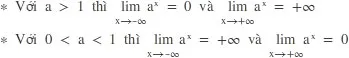Đáp Án Thủ Thuật về Các dạng bài tập khảo sát sự biến thiên và vẽ đồ thị hàm số 2022
You đang tìm kiếm từ khóa Các dạng bài tập khảo sát sự biến thiên và vẽ đồ thị hàm số được Update vào lúc : 2022-02-25 10:40:23 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo Post vẫn ko hiểu thì có thể lại bình luận ở cuối bài để Ad giải thích và hướng dẫn lại nha.
Trang chủ Lớp 12 Toán lớp 12 Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số Phương pháp khảo sát sự biến thiên và vẽ đồ thị hàm số
Toán lớp 12
Nội dung chính
- Phương pháp khảo sát sự biến thiên và vẽ đồ thị hàm sốCó thể bạn quan tâm Bài 6 trang 44 SGK Giải tích 12 Bài 7 trang 44 SGK Giải tích 12 Bài 8 trang 44 SGK Giải tích 12 Bài 9 trang 44 SGK Giải tích 12 Video liên quan
PHẦN GIẢI TÍCH – TOÁN 12
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Bài 1. Sự đồng biến, nghịch biến của hàm số
Bài 2. Cực trị của hàm số
Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 4. Đường tiệm cận
Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Ôn tập Chương I – Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm sô
CHƯƠNG II. HÀM SỐ LŨY THỪA HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Bài 1. Lũy thừa
Xem Thêm
Phương pháp khảo sát sự biến thiên và vẽ đồ thị hàm số
Phương pháp khảo sát sự biến thiên và vẽ đồ thị hàm số
Để đáp ứng nhu cầu học tập và rèn luyện tham khảo thêm chuyên đềkhảo sát và vẽ đồ thị hàm số cho các em,cùng học vuixin giới thiệu một tài liệu rất thú vị về chương họcmà được rất nhiều các bạn học sinh quan tâm. Bài viết chắc chắn sẽ đem lại cho bạn đọc những điều bổ ích. Hãy cùng chúng tôi khám phá nhé!
I. Khảo sát sự biến thiên
Các bước khảo sát sự biến thiên của hàm số:
Bước 1: Tìm tập xác định của hàm số. Xét tính chẵn, lẻ, tuần hoàn của hàm số để thu hẹp phạm vi khảo sát.
Bước 2: khảo sát và lập bảngbiến thiên :
+ Xét sự biến thiên của hàm số :
– Tìm đạo hàm bậc nhất y’ ;
– Tìm các điểm tại đó y’ bằng 0 hoặc không xác định ;
– Xét dấu y’ và suy ra chiều biến thiên của hàm số .
+ Tìm cực trị .
+ Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có).
+ Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị.
II. Cách vẽ đồ thị hàm số
Các dạng đồ thị hàm số: Chủ yếu là đồ thị hàm số mũ
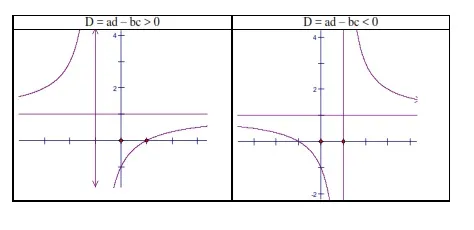
1. Đồ thị hàm số bậc nhất
- Xét chiều biến thiên của hàm số
+ Tính đạo hàm
+ Lập bảng xét dấu y
+ Hàm số đồng biến (nghịch biến) trên các khoảng và
- Tìm cực trị:Hàm số đã cho không có cực trị Tiệm cận:
Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
- Đồ thị hàm số y= ax+b
-Giao của đồ thị với trục Oy: x = 0 =>y = => (0; )
– Giao của đồ thị với trục Ox: Giải phương trình y = 0
– Lấy thêm một số điểm (nếu cần)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
– Nhận xét về đặc trưng của đồ thị. Đồ thị nhận điểm là giao hai đường tiệm cận làm tâm đối xứng.
2. Cách vẽ đồthị hàm số bậc 2
Vẽ đồ thị hàm bậc 2: Đồ thị hàm số y=ax2.
Vẽ đồ thị hàm số bậc 2là hàm số có dạng (y = ax^2+ bx + c,) trong đó a, b, c là các hằng số và a 0.
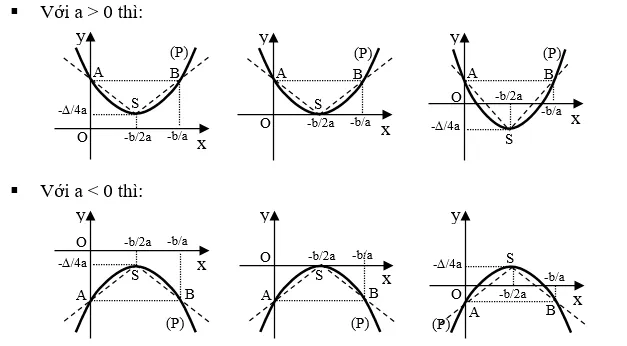
Đồ thị hàm số bậc hai: đồ thị của hàm số là một Parabol (P) có các dạng:
- Hướng bề lõm lên trên nếu a > 0. Hướng bề lõm xuống dưới nếu a < 0.
Để vẽ đồ thị hàm số bậc hai chúng ta không thực hiện các phép tịnh tiến từ đồ thị hàm số ta thực hiện như sau:
- Lấy ba điểm chủ đạo, gồm đỉnh S và hai điểm A, B đối xứng với nhau qua S. Nối ASB để được một góc rồi thực hiện vẽ đường cong parabol lựon theo đường góc này.
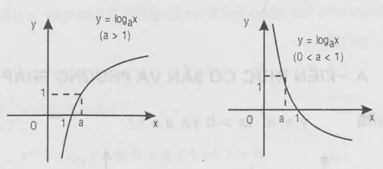
3. Đồ thị hàm số logarit
(y = log_a^x (0 < a, a 1) )
Tập xác định (D = (0 ; +), y = log_a^x) nhận mọi giá trị trong R.
Hàm số đồng biến trên R khi a > 1 và nghịch biến trên R khi 0 < a 1.
Đồ thị qua điểm (1 ; 0), nằm bên phải trục tung và nhận trục tung làm tiệm cận đứng.
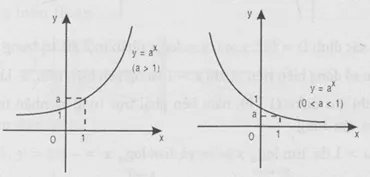
4. Hàm số mũ
(y = a^x(a > 0 và a 1))
Tập xác định(D = R, y = a^x> 0, x R.)
Hàm số đồngbiến trên R khi a > 0, nghịch biến trên R khi 0 < a < 1.
Đồthị qua điểm (0 ; 1), nằm phía trên trục hoành và nhận trục hoành làm tiệm cận ngang.
Đạo hàm :
- (y = a^x có y = a^xlna) (y = e^x có y = e^x ) Với u(x) là hàm sốtheo X có đạo hàm là u(x) thì:(y = a^u có y’ = a^u.u’ .lna và y = e^u có y’ = e^u.u’ .)
Xem thêm:
- Tổng hợp lý thuyết và bài tập đường tiệm cận của hàm số Tổng hợp đầy đủ những giới hạn hay gặp mà học sinh không thể bỏ qua Tổng hợp đầy đủ những công thức giới hạn học sinh không nên bỏ qua Giới hạn Các giới hạn hay gặp
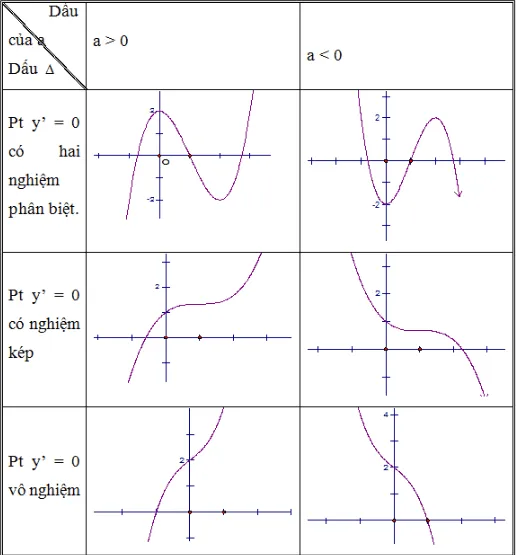
5. Đồ thị hàm số bậc 3
Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc 3:(y = ax^3+ bx^2+ cx + d (aneq0))
6. Đồ thị hàm số bậc 4
Phần này ta sẽ tìm hiểu cách vẽ đồ thị hàm số bậc 4 dưới dạng hàm số trùng phương nhưsau:
Lập bảng biến thiên và vẽ đồ thị hàm số:(y=ax^4+bx^2+c)
Để vẽ được đồ thị dạng này ta đặt(x^2=t). Phương trình cũ trở thành phương trình bậc hai có dạng:(^2+bt+c=0). áp dụng tương tự cách vẽ đồ thị hàm bậc hai như trên.
Có thể bạn quan tâm:
- Nguyên hàm Giới hạn Bộ công thức đạo hàm chuẩn, đầy đủ nhất dành cho các bạn học sinh THPT
7. Tìm tâm đối xứng của đồ thị hàm số
Chứng minh rằng đồ thị hàm số y = f(x) nhận điểm I(a, b) làm tâm đối xứng, ta thực hiện theo các bước sau:
Bước 1:Với phép biến đổi toạ độ:
(left{ beginarraylX = x – a\Y = y – bendarray right.)
(Rightarrow left{ beginarraylx = X + a\y = Y + bendarray right.)
hàm số có dạng: (Y + b = f(X + a) Rightarrow Y = F(X) (1))
Bước 2:Nhận xét rằng hàm số (1) là hàm số lẻ.
Bước 3:Vậy, đồ thị hàm số nhận điểm I(a, b) làm tâm đối xứng.
Bài tập trắc nghiệm nhận dạng đồ thị hàm số:Một số bài toán thường gặp về đồ thị.
Trên đây là bản tổng hợp đầy đủ nhất về chương khảo sát và vẽ đồ thị hàm số, hy vọng nó giúp bạn hiểu rõ về các dạng kiến thức trong học phần này. Chúng tôi tin rằng chỉ cần có sự đầu tư thời gian thì chúng sẽ không thể làm khó được bạn. Chúc các bạn thành công!
Tags bài tập trắc nghiệm nhận dạng đồ thị hàm số lập bảng biến thiên và vẽ đồ thị hàm số đồ thị hàm số bậc 4 Bài trước
Có thể bạn quan tâm
Bài 6 trang 44 SGK Giải tích 12
Bài 7 trang 44 SGK Giải tích 12
Bài 8 trang 44 SGK Giải tích 12
Bài trước
Bài 9 trang 44 SGK Giải tích 12
Bạn muốn xem thêm với
- Câu hỏi 5 trang 38 SGK Giải tích 12 Bài 1 trang 43 SGK Giải tích 12 Bài 2 trang 43 SGK Giải tích 12 Bài 3 trang 43 SGK Giải tích 12 Bài 4 trang 44 SGK Giải tích 12 Bài 5 trang 44 SGK Giải tích 12 Bài 6 trang 44 SGK Giải tích 12 Bài 7 trang 44 SGK Giải tích 12 Bài 8 trang 44 SGK Giải tích 12 Bài 9 trang 44 SGK Giải tích 12 Câu hỏi 1 trang 32 SGK Giải tích 12
Reply
3
0
Chia sẻ
![]()
Review Các dạng bài tập khảo sát sự biến thiên và vẽ đồ thị hàm số ?
Bạn vừa Read Post Với Một số hướng dẫn một cách chi tiết hơn về Review Các dạng bài tập khảo sát sự biến thiên và vẽ đồ thị hàm số mới nhất
Share Link Down Các dạng bài tập khảo sát sự biến thiên và vẽ đồ thị hàm số miễn phí
Người Hùng đang tìm một số Chia SẻLink Download Các dạng bài tập khảo sát sự biến thiên và vẽ đồ thị hàm số Free.
Hỏi đáp thắc mắc về Các dạng bài tập khảo sát sự biến thiên và vẽ đồ thị hàm số
Nếu You sau khi đọc bài viết Các dạng bài tập khảo sát sự biến thiên và vẽ đồ thị hàm số , bạn vẫn chưa hiểu thì có thể lại Comment ở cuối bài để Ad giải thích và hướng dẫn lại nha
#Các #dạng #bài #tập #khảo #sát #sự #biến #thiên #và #vẽ #đồ #thị #hàm #số