Giải Giải toán lớp 7 sách bài tập 2022

Giải Kinh Nghiệm về Giải toán lớp 7 sách bài tập Mới Nhất

Pro đang tìm kiếm từ khóa Giải toán lớp 7 sách bài tập được Cập Nhật vào lúc : 2022-04-04 06:35:20 . Với phương châm chia sẻ Bí kíp về trong bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì có thể lại Comment ở cuối bài để Mình giải thích và hướng dẫn lại nha.

Câu 6 trang 19 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho biểu thức (5rmx^2 + 3rmx – 1). Tính giá trị của biểu thức tại:

a) x = 0

b) x = – 1

c) (x = 1 over 3)

Giải

a) Thay x = 0 vào biểu thức ta có:

$$5.0^2 + 3.0 – 1 = 0 + 0 – 1 = – 1$$

Vậy giá trị của biểu thức (5rmx^2 + 3rmx – 1) tại x = 0 là -1

b) Thay x = -1 vào biểu thức ta có:

$$5.left( – 1 right)^2 + 3.left( – 1 right) – 1 = 5.1 – 3 – 1 = 1$$

Vậy giá trị của biểu thức (5rmx^2 + 3rmx – 1) tại x = -1 là 1.

c) Thay (x = 1 over 3) vào biểu thức ta có:

$$5.left( 1 over 3 right)^2 + 3.1 over 3 – 1 = 5.1 over 9 + 1 – 1 = 5 over 9$$

Vậy giá trị của biểu thức (5rmx^2 + 3rmx – 1) tại (x = 1 over 3) là (5 over 9)

Câu 7 trang 19 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Tính giá trị của các biểu thức sau:

a) 3x – 5y +1 tại (x = 1 over 3;y = – 1 over 5)

b) (3rmx^2 – 2rmx – 5) tại (rmx = 1;x = – 1;x = 5 over 3)

c) (rmx – 2y^2 + z^3) tại x = 2; y = -1; z = -1

Giải

a) Thay (x = 1 over 3;y = – 1 over 5) vào biểu thức ta có:

(3.1 over 3 – 5.left( – 1 over 5 right) + 1 = 1 + 1 + 1 = 3)

Vậy giá trị của biểu thức 3x – 5y +1 tại (rmx = 1 over 3) và (y = – 1 over 5) là 3.

b) Thay x = 1 vào biểu thức ta có:

(3.1^2 – 2.1 – 5 = 3 – 2 – 5 = – 4)

Vậy giá trị của biểu thức (3rmx^2 – 2rmx – 5) tại x = 1 là -4

Thay x = -1 vào biểu thức ta có:

(3.( – 1)^2 – 2.( – 1) – 5 = 3 – 2 – 5 = – 4)

Vậy giá trị của biểu thức (3rmx^2 – 2rmx – 5) tại x = -1 là 0.

Thay (x = 5 over 3) vào biểu thức ta có:

(3.left( 5 over 3 right)^2 – 2.5 over 3 – 5 = 3.25 over 9 – 10 over 3 – 5 = 25 over 3 – 10 over 3 – 15 over 3 = 0)

Vậy giá trị của biểu thức (3rmx^2 – 2rmx – 5) tại (x = 5 over 3) là 0.

c) Thay x = 4, y = -1 vào biểu thức ta có:

(4 – 2.left( – 1 right)^2 + left( – 1 right)^3 = 4 – 2.1 + ( – 1) = 4 – 2 – 1 = 1)

Vậy giá trị của biểu thức (rmx – 2y^2 + z^3) tại x = 4, y = -1, z = -1 là 1.

Câu 8 trang 20 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Tính giá trị của biểu thức sau.

a) (rmx^2 – 5rmx) tại (rmx = 1;x = – 1;x = 1 over 2)

b) (3rmx^2 – xy) tại x = -3; y = -5

c) (5 – xy^3) tại x = 1; y = -3

Giải

a) Thay x = 1 vào biểu thức ta có:

$$1^2 – 5.1 = 1 – 5 = – 4$$

Vậy giá trị của biểu thức (rmx^2 – 5rmx) tại x = 1 là -4

Thay x = -1 vào biểu thức ta có:

$$( – 1)^2 – 5.( – 1) = 1 + 5 = 6$$

Vậy giá trị của biểu thức (rmx^2 – 5rmx) tại x = -1 là 6

Thay (rmx = 1 over 2) vào biểu thức ta có:

$$left( 1 over 2 right)^2 – 5.1 over 2 = 1 over 4 – 10 over 4 = – 9 over 4$$

Vậy giá trị của biểu thức (rmx^2 – 5rmx) tại (rmx = 1 over 2) là (- 9 over 4)

b) Thay x = -3 và y = – 5 vào biểu thức ta có:

$$3.left( – 3 right)^2 – ( – 3).( – 5) = 3.9 – 15 = 12$$

Vậy giá trị của biểu thức (3rmx^2 – xy) tại x = -3; y = -5 là 12

c) Thay x = 1, y = -2 vào biểu thức ta có:

$$5 – 1.( – 3)^3 = 5 – 1.( – 27) = 5 + 27 = 32$$

Vậy giá trị của biểu thức (5 – xy^3) tại x = 1; y = -3 là 32

Giaibaitap.me

Page 2

Giải bài III.5, III.6, III.7, III.8 trang 54 Sách… Giải bài III.1, III.2, III.3, III.4 trang 54 Sách… Giải bài 89, 90, 91 trang 53, 54 Sách Bài Tập… Giải bài 86, 87, 88 trang 53 Sách Bài Tập Toán… Giải bài 82, 83, 84, 85 trang 52, 53 Sách Bài Tập… Giải bài 9.4, 9.5, 9.6 trang 52 Sách Bài Tập Toán… Giải bài 78, 79, 80, 81 trang 51 Sách Bài Tập… Giải bài 74, 75, 76, 77 trang 51 Sách Bài Tập… Giải bài 9.1, 9.2, 9.3 trang 51, 52 Sách Bài Tập… Giải bài 70, 71, 72, 73 trang 50, 51 Sách Bài Tập…

Page 3

Page 4

Page 5

Page 6

Page 7

Page 8

Page 9

Page 10

Page 11

Page 12

Page 13

Page 14

Page 15

Page 16

Page 17

Page 18

Page 19

Page 20

Page 21

Page 22

Câu 5 trang 36 Sách Bài Tập (SBT) Toán lớp 7 tập 2

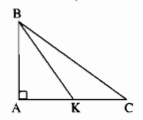
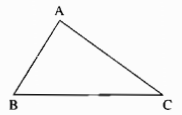
Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh các độ dài BK, BC.

Giải

Trong ∆ACK ta có (widehat BKC) là góc ngoài tại đỉnh K.

(widehat BKC > widehat A = 90^circ ) (tính chất góc ngoài)

Trong ∆BKC ta có (widehat BKC) là góc tù, BC là cạnh đối diện với (widehat BKC) nên BC > BK

Câu 1.1, 1.2, 1.3 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Câu 1.1 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Tam giác ABC có Â là góc tù, (widehat B > widehat C). Trong các khẳng định sau, khẳng định nào đúng?

(A) AB > AC > BC (B) AC > AB > BC

Giải

Do Â là góc tù nên Â lớn nhất. Vậy có (widehat A > widehat B > widehat C). Từ đó suy ra BC > AC > AB. Chọn (D) BC > AC > AB.

Câu 1.2 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Tam giác ABC có AB = 5cm, BC = 6cm và AC = 7cm. Gọi (widehat A_1,widehat B_1,widehat C_1) theo thứ tự là góc ngoài tại đỉnh A, B, C của tam giác đó. Trong các khẳng định sau, khẳng định nào đúng?

(left( A right)widehat A_1 > widehat B_1 > widehat C_1)

(left( B right)widehat B_1 > widehat C_1 > widehat A_1)

(left( C right)widehat C_1 > widehat A_1 > widehat B_1)

(left( D right)widehat C_1 > widehat B_1 > widehat A_1)

Giải

Ta có (widehat A_1 = 180^circ – widehat A;widehat B_1 = 180^circ – widehat B;widehat C_1 = 180^circ – widehat C). Theo giả thiết ta có AB < BC < AC. Từ đó suy ra (widehat C < widehat A < widehat B). Vậy (widehat C_1 > widehat A_1 > widehat B_1).

Chọn (left( C right)widehat C_1 > widehat A_1 > widehat B_1)

Câu 1.3 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

So sánh các cạnh của một tam giác cân, biết rằng nó có một góc ngoài bằng 40°.

Giải

Theo giả thiết, tam giác cân này có một góc ngoài bằng 40° nên nó có một góc trong bằng 180° – 40° = 140°. Góc trong này không thể là góc ở đáy của tam giác cân mà phải là góc ở đỉnh. Vậy cạnh đáy của tam giác cân lớn hơn hai cạnh bên của nó.

Giaibaitap.me

Page 23

Câu 1.4, 1.5, 1.6 trang 37, 38 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Câu 1.4 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC với AB ≥ AC. Trên cạnh BC lấy một điểm M bất kỳ khác B và C. Chứng minh rằng AM < AC.

Giải

Ta có (widehat M_1 + widehat M_2 = 180^circ ) nên chỉ có hai khả năng xảy ra ứng với các vị trí của M trên BC là (widehat M_1 > 90^circ ) hoặc (widehat M_2 ge 90^circ ).

– Nếu (widehat M_1 > 90^circ ) thì tam giác AMC có góc tù nên AM > AC

– Nếu (widehat M_2 ge 90^circ ) thì trong tam giác ABM có AM < AB. Kết hợp với giả thiết AB < AC, ta suy ra AM < AC. Vậy ta luôn có AM < AC.

Câu 1.5 trang 38 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC với AB ≤ BC ≤ CA. Trên các cạnh BC và AC lần lượt lấy hai điểm M và N (khác A, B, C). Chứng minh rằng MN < AC.

Giải

Kẻ đoạn thẳng AM. Xét tam giác MAC. Chứng minh tương tự như bài 1.4 ta có MN < a, trong đó a là đoạn lớn nhất trong hai đoạn thẳng MA và MC. Nếu ta chứng minh được

MA < AC và MC < AC thì sẽ suy ra được a < AC, từ đó có MN < AC.

Trong tam giác ABC có AB ≤ AC, M ∈ BC (M # B, M # C); Chứng minh tương tự bài 1.4, ta có AM < AC. Mặt khác MC < BC ≤ CA. Vậy a < AC, suy ra MN < AC.

Câu 1.6 trang 38 Sách Bài Tập (SBT) Toán lớp 7 tập 2

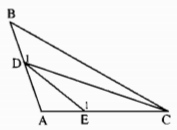
Cho tam giác ABC có góc A tù. Trên cạnh AB lấy điểm D (khác A và B), trên cạnh AC lấy điểm E (khác A và C). Chứng minh rằng DE < BC.

Giải

Xét tam giác CDE. Ta có (widehat E > widehat A), mà Â là góc tù nên (widehat E_1) là góc tù.

Suy ra CD > DE (1)

Xét tam giác BCD. Ta có (widehat D_1 > widehat A) nên (widehat D_1) là góc tù.

Suy ra BC > CD (2)

Từ (1) và (2) suy ra BC > DE.

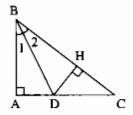
Câu 6 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh các độ dài AD, DC

Giải

Kẻ (DH bot AC)

Xét hai tam giác vuông ABD và BHD:

(widehat B_1 = widehat B_2left( gt right))

Cạnh huyền BD chung.

Do đó: ∆ABD = ∆HBD (cạnh huyền góc nhọn)

( Rightarrow ) AD = HD (2 cạnh tương ứng) (1)

Trong tam giác vuông DHC có (widehat DHC = 90^circ )

( Rightarrow ) DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)

Từ (1) và (2) suy ra: AD < DC

Giaibaitap.me

Page 24

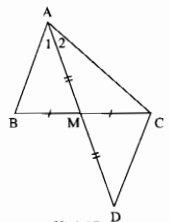
Câu 7 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

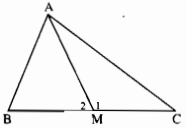
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. So sánh (widehat BAM) và (widehat CAM).

Giải

Trên tia đối tia MA lấy điểm D sao cho MD = MA.

Xét ∆AMB và ∆DMC:

MA = MD (theo cách vẽ)

(widehat AMB = widehat DMC) (đối đỉnh)

MB = MC (gt)

Do đó: ∆AMB = ∆DMC (c.g.c)

Nên: AM = CD (2 cạnh tương ứng)

(widehat D = widehat A_1) (2 góc tương ứng) (1)

AB < AC (gt)

Suy ra: CD < AC

Trong ∆ADC ta có: CD < AC

Nên (widehat D = widehat A_2) (đối diện cạnh lớn hơn là góc lớn hơn) (2)

Từ (1) và (2) suy ra: (widehat A_1 = widehat A_2) hay (widehat BAM > widehat MAC)

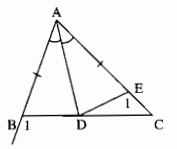
Câu 8 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở D. So sánh các độ dài BD, DC.

Giải

Trên cạnh AC lấy điểm E sao cho AE = AB

AB < AC nên AE < AC => E nằm giữa A và C

Xét ∆ABD và ∆AED:

AB = AE (theo cách vẽ)

(widehat BArmD = widehat ErmADleft( gt right))

AD cạnh chung

Do đó: ∆ABD = ∆AED (c.g.c)

=> BD = DE (2 cạnh tương ứng)

( Rightarrow widehat ABrmD = widehat ArmED) (2 góc tương ứng)

(widehat ABrmD + widehat B_1 = 180^circ ) (2 góc kề bù)

(widehat ArmED + widehat E_1 = 180^circ ) (2 góc kề bù)

Suy ra: (widehat B_1 = widehat E_1)

Trong ∆ABC ta có (widehat B_1) là góc ngoài tại đỉnh B.

( Rightarrow widehat B_1 > widehat C) (tính chất góc ngoài tam giác)

Suy ra: (widehat E_1 > widehat C)

Trong ∆DEC ta có: (widehat E_1 > widehat C)

( Rightarrow ) DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)

Suy ra: BD < DC.

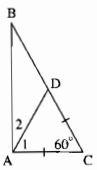
Câu 9 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Chứng minh rằng nếu một tam giác vuông có một góc nhọn bằng 30° thì cạnh góc vuông đối diện với nó bằng nửa cạnh huyền.

Giải

Xét ∆ABC có (widehat A = 90^circ ;widehat B = 30^circ )

Trên cạnh BC lấy điểm D sao cho CD = AC

Suy ra: ∆ACD cân tại C

Mà (widehat C + widehat B = 90^circ ) (tính chất tam giác vuông)

( Rightarrow widehat C = 90^circ – widehat B = 90^circ – 30^circ = 60^circ )

Suy ra: ∆ACD đều

( Rightarrow ) AC = AD = DC và (widehat A_1 = 60^circ )

(widehat A_1 + widehat A_2 = widehat BAC = 90^circ Rightarrow widehat A_2 = 90^circ – widehat A_1 = 90^circ – 60^circ = 30^circ )

Trong ∆ADB ta có: (widehat A_2 = widehat B = 30^circ )

Suy ra: ∆ADB cân tại D (vì có 2 góc kề cạnh AB bằng nhau)

( Rightarrow ) AD = DB

Suy ra: AC = CD = DB mà CD + DB = BC

Vậy (AC = 1 over 2BC)

Câu 10 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Chứng minh rằng định lý “Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn” theo gợi ý sau:

Cho tam giác ABC có (widehat B > widehat C)

a) Có thể xảy ra AC < AB hay không ?

b) Có thể xảy ra AC = AB hay không ?

Giải

a) Nếu AB > AC thì (widehat C > widehat B) (góc đối diện với cạnhlớn hơn là góc lớn hơn)

Điều này trái với giả thiết (widehat B > widehat C)

b) Nếu AB = AC thì ∆ABC cân tại A.

(Rightarrow widehat B = widehat C) (tính chất tam giác cân)

Điều này trái với giả thiết (widehat B > widehat C)

Vậy: (widehat B > widehat C) thì AC > AB

Giaibaitap.me

Page 25

Câu 11 trang 38 Sách Bài Tập (SBT) Toán lớp 7 tập 2

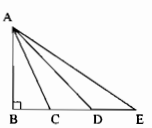
Cho hình sau. So sánh độ các độ dài AB, AC, AD, AE.

Giải

Điểm C nằm giữa B và D nên BC < BD (1)

Điểm C nằm giữa B và E nên BD < BE (2)

Vì B, C, D, E thẳng hàng. Từ (1) và (2) suy ra

BC < BD < BE

(AB bot BE)

Suy ra: AB < AC < AD < AE.

Câu 12 trang 38 Sách Bài Tập (SBT) Toán lớp 7 tập 2

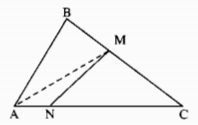
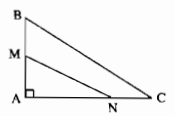
Cho hình bên. Chứng minh rằng MN < BC

Giải

Nối BN

Vì M nằm giữa A và B nên AM < AB

$$NA bot AB$$

Suy ra: NM < NB (đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn) (1)

Vì N nằm giữa A và C nên AN < AC

$$BA bot AC$$

Suy ra: BN < BC (đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn) (2)

Từ (1) và (2) suy ra: MN < BC.

Câu 13 trang 38 Sách Bài Tập (SBT) Toán lớp 7 tập 2

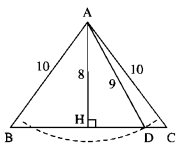
Cho tam giác ABC cân tại A có AB = AC = 10cm, BC = 12cm. Vẽ cung tròn tâm A có bán kính 9cm. Cung đó có cắt đường thẳng BC hay không có cắt cạnh BC hay không? Vì sao?

Giải

(AH bot BC)

(widehat AHB = widehat AHC = 90^circ )

(HB = HC = BC over 2 = 6left( cm right))

(widehat AHB = 90^circ )

(eqalign & AB^2 = AH^2 + HB^2 cr & AH^2 = AB^2 – HB^2 cr & AH^2 = 10^2 – 6^2 = 64 cr

& AH > 0 Rightarrow AH = 8left( cm right) cr )

Do bán kính cung tròn 9 (cm) > 8 (cm) nên cung tròn tâm A bán kính 9 cm cắt đường thẳng BC. Gọi D là giao điểm của cung tròn tâm A bán kính 9 cm. Với BC ta có đường xiên AD > AC nên hình chiếu HD < HC do đó D nằm giữa H và C. Vậy cung tròn tâm A bán kính 9cm cắt cạnh BC.

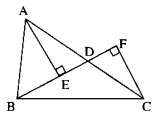
Câu 14 trang 38 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BD. So sánh AC với tổng AE + CF.

Giải

Trong ∆ADE ta có (widehat ArmED = 90^circ )

Nên AE < AD (1)

Trong ∆CFD ta có (widehat CFrmD = 90^circ )

Nên CF < CD (2)

Cộng từng vế (1) và (2) ta có:

AE + CF < AD + CD

Mà D nằm giữa A và C nên AD + CD = AC

Vậy AE + CF < AC

Giaibaitap.me

Page 26

Clip Giải toán lớp 7 sách bài tập ?

Bạn vừa tham khảo Post Với Một số hướng dẫn một cách chi tiết hơn về Video Giải toán lớp 7 sách bài tập mới nhất

Share Link Tải Giải toán lớp 7 sách bài tập miễn phí

Bạn đang tìm một số Share Link Down Giải toán lớp 7 sách bài tập miễn phí.

Giải đáp thắc mắc về Giải toán lớp 7 sách bài tập

Nếu Bạn sau khi đọc bài viết Giải toán lớp 7 sách bài tập , bạn vẫn chưa hiểu thì có thể lại bình luận ở cuối bài để Tác giả giải thích và hướng dẫn lại nha
#Giải #toán #lớp #sách #bài #tập